


Four representative applications were investigated in this category: a molecular reaction modeling problem, global climate modeling, chemical process optimization, and branch and bound combinatorial problems. In most cases, the time for obtaining results for interesting problem sizes on a single machine ranged from several hours to weeks using the fastest supercomputer available at the beginning of the project, with the problem size and/or accuracy of the results correspondingly constrained.
The nature of the first three applications allowed a functional distribution of key software components, enabling the possibility of superlinear speedups through the use of heterogeneous computer architectures, and such speedups were in fact realized during the project.
Even for cases limited to linear speedups due to problem homogeneity or because computer architecture did not make a significant difference, the resulting speedups enabled a major advance in the amount and quality of data which could be obtained. And beyond the speedup factor, testbed experience revealed or confirmed a number of other benefits of metacomputing, foremost among them the ability to take advantage of already-installed software and local expertise at a site, rather than having to port the software to another site.
Having said this, software development and porting did in fact account for a major part of testbed application activities. One reason for this was that MIMD MPP machines were not available on a production basis prior to the start of the project, precluding the use of existing application software which took advantage of the new machine architectures. A second reason was that most existing software was written for execution on a single machine, and so needed to be partitioned for distributed execution over a wide area network. Gaining an understanding of how to partition applications for heterogeneous metacomputing was in fact one of the key goals of the testbed applications research, and accounted for much researcher time in the early phases of the project.
Two important dimensions common to the applications of this group are problem size and computational granularity. Measures for problem size are specific to the type of problem, for example the number of simulated years and spatial resolution used in a global climate modeling computation. Computational granularity is a measure of the incremental computation associated with network data transfers for a given problem size.
For problems involving two-way (or n-way) interchange dependencies, one would like to find maximal speedup distributions with computational granularities which are much larger than network propagation times, thus negating speedup degradations due to speed-of-light latencies. For many problems, achieving this for the maximum-size problems which can be run with present processing power implies continuing to achieve it as processing power increases, since researchers will eagerly increase the problem size to use the new capacity.
In the following, the quantum chemical dynamics application is an example of a one-way pipeline flow in which computational granularity need not be large compared to propagation time (providing the right choices are made for the associated communication protocols). In the global climate model application, on the other hand, processing is sequentially dependent on interchanges in both directions between its distributed components, and as a result is directly impacted by propagation time.
This application provides an example of basic scientific investigation through computer modeling. The objective is to predict the rates and cross-sections of chemical reactions from first principles using quantum mechanics, providing an understanding of chemical reactions at the molecular level. The work was carried out in the Casa testbed by researchers at Caltech, using supercomputers at all four Casa sites over the course of the project.
The problem solution consists of three steps: local hyperspherical surface function (LHSF) calculations, log-derivative (LOG-D) propagation calculations, and asymptotic (ASY) analysis. The first two steps are centered on matrix calculations and require large amounts of machine time for matrix diagonalization, inversion, and multiplication. The third step is not computationally intensive, and can be done in series with the other steps without impacting the total solution time.
The measure for problem size here is the number of "channels" used for the computation, with the number of channels directly determining matrix size. The channels represent the number of molecular rotational and vibrational states used in the modeling, which determines the level of detail obtained in the results. Typical problem sizes in the tested work involved on the order of 1000 channels.
This problem involves a small amount of data input, e.g. the initial conditions and size parameters, and large amounts of data output, in the range of hundreds of Megabytes to Gigabytes. Its computational structure made it a good candidate for heterogeneous metacomputing, since the LHSF and LOG-D steps provided natural architecturally-related partitioning choices. The intensive part of LHSF computation involved matrix diagonalizations, which was well-matched to vector processing, while LOG-D computation involved primarily matrix inversions and multiplications, which could be done efficiently on MPP machines (Figure 4-18).
Figure 4-18. Quantum Chemical Dynamics
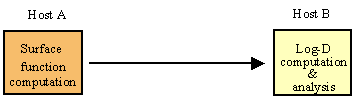
A one-way pipelined distribution (Figure 4-17B) was developed by Caltech researchers in which a set of LHSF matrix calculations for a single hyperspherical sector were performed on a vector machine and the results sent to an MPP machine for LOG-D processing. Once the first sector's data was sent, both machines could then perform computations in parallel using this pipeline. When all matrix computations were completed, ASY processing was then carried out on the MPP machine.
Using a 1000-channel problem size, a single Cray YMP CPU at SDSC with a processing power of 0.2 Gflops, and a 64-node Intel Delta configuration at Caltech, a 5 Mbps data rate (the Delta's maximum I/O rate) allowed LHSF data to be transferred and the next LHSF computation to be completed in parallel with an incremental LOG-D computation. Using an analytical model to extrapolate this work to two machines with a processing power of 10 Gflops each, a 900 Mbps data rate would allow the problem size to be increased to 3700 channels and the pipeline again kept full.
To determine the resulting speedup, the wall-clock time for the distributed solution was compared to the wall-clock times which resulted when all execution was done on each machine alone. The problem required 29 hours to run on the single Cray C90 CPU and 28 hours on the 64-node Intel Delta. With the problem partitioned among the two machines as described above, total execution time was 8.5 hours, resulting in a superlinear speedup factor of 3.3.
In a later set of three-machine experiments, a single-processor Cray YMP located at LANL shared the LHSF processing task with an 8-processor configuration of the C90 at SDSC, while LOG-D processing was done using 128 nodes of an Intel Paragon at Caltech. Using a problem size of 512 channels, a speedup factor of 2.85 was achieved. This non-superlinear result was attributed to the imbalance of computational loads due to the relatively low-powered LANL machine used in the configuration.
To provide a comparison to the experimental results, a detailed analytical model was developed by Caltech and used to predict expected speedup gains as a function of problem and machine configuration variables. For the two-machine case the model gave excellent agreement with experimental results for a wide range of problem sizes. In the three-machine case, experimental speedup gains were about 20% less than the model's predictions due to its balanced-load assumption.
In summary, the quantum chemical dynamics work confirmed the superlinear speedup capability of wide area metacomputing and dramatically reduced the time required to solve an important class of problems, significantly advancing computational modeling capabilities for fundamental science. As proof of its effectiveness, the increased accuracy provided by the testbed experiments produced new results concerning the geometric phase effect in hydrogen reactions [4].
This application, investigated by UCLA, SDSC, and LANL in the Casa testbed, has as its objective the prediction of long-term changes to the earth's climate through the use of atmospheric and ocean computer models. Each of the models is a large software program reflecting many years of development, and each incorporates a large body of theoretical and empirical knowledge. Several different programs have been developed over time by different groups of researchers for execution on particular machines.
Because the atmosphere and oceans strongly influence each other, the model for one must exchange data with the model for the other as the computation proceeds. The problem size for this application is determined by the spatial resolution used and the number of calendar years of time simulated by the coupled models.
Much of the Casa work was based on an atmospheric general circulation model (AGCM) developed at UCLA and an ocean general circulation model (OGCM) developed at Princeton. The problem resolution used with these programs was 5 degrees longitude, 4 degrees latitude, and 9 atmospheric levels for the AGCM, and 1 degree longitude, 0.3 degrees latitude, and 40 depth levels for the OGCM.
A second ocean model developed at LANL was also used in Casa later in the project in conjunction with the UCLA AGCM model. Called the Parallel Ocean Program (POP), it was developed specifically for execution on LANL's CM-5 MPP to provide higher-resolution simulations. Using 256 nodes of the CM-5, the POP could provide ocean modeling resolutions of 0.28 degrees longitude and 0.17 degrees average latitude with 20 depth levels.
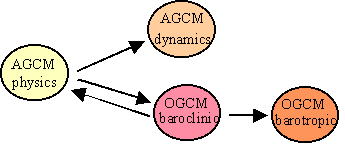
The AGCM and OGCM programs provided a natural starting point for distributing the global climate modeling problem among the nodes of a metacomputer, since they were already separately implemented and had well-defined data exchange interfaces. However, each of these programs could also be readily decomposed into two functions, yielding a total of four distinct components: AGCM Physics, AGCM Dynamics, OGCM Baroclinic, and OGCM Barotropic. These components had significantly different machine-dependent execution times. For example, the AGCM Physics and Princeton OGCM components ran about a factor of three faster on the MPP architecture of the Intel Paragon than on a vector-based Cray C90 CPU, whereas the AGCM Dynamics was faster on the C90.
An important logical constraint on possible component distributions was imposed by the problem's data exchange requirements. The results of an AGCM Physics incremental computation had to be passed to the AGCM Dynamics and OGCM Baroclinic components before the latter could proceed with their computations, and the Baroclinic results had to be passed to the Physics and Barotropic components before they could proceed with their next computations (Figure 4-19). Thus a two-way sequential exchange was required between the Physics and Baroclinic components, constraining parallelism choices and making network latency a potentially limiting factor in the speedup which could be achieved.
Figure 4-19. Global Climate Modeling Exchanges
Fortunately, the incremental computation intervals for the C90-Paragon distribution were on the order of 1-2 seconds, making network speed-of-light latency insignificant. For the problem size used, if there was no overlap of computation and communication, the amounts of data exchanged required a transmission data rate on the order of 100 Mbps or higher to keep total network latency from adding significantly to solution wall-clock time. If the problem resolution and processing speed is increased, the network data rate must also be increased to maintain this result.
On the other hand, if data generation is spread out over the computation interval, the data can be sent in parallel with the computation and the data rate requirement correspondingly reduced. As part of their work, UCLA researchers developed a subdomain computation method which did in fact allow communications to take place in parallel with computation.
Taking all of these factors into account and using a configuration consisting of one CPU on the C90 at SDSC and 242 nodes on the Paragon at Caltech, a speedup of 1.55 was obtained using the best possible component distribution. The total time to run all components on only the Paragon was 9.5 hours per simulated year, which was reduced to 6.2 hours/year using both machines. Further reductions in total solution time became possible in the latter part of the project when a Cray T3D was installed at JPL. Using a combination of measurements and estimated speedups for individual components, the estimated solution time with all components running on the T3D was 6.6 hours/year. By distributing the components among the T3D and two CPUs on the SDSC C90, a total estimated solution time of 2.9 hours/year and speedup of 2.2 was obtained.
The metacomputing results for this application, while not achieving significant superlinear speedups, nevertheless can be seen to give significant reductions in solution wall-clock time. Of perhaps equal importance is the ability to couple improved-resolution models such as LANL's POP, developed explicitly for execution on the CM-5, with the UCLA or other atmospheric models. For this problem class, the enabling of collaboration-at-a-distance among research groups working different aspects of the problem may outweigh the absence of dramatic speedup gains.
In related work done by SDSC for the GCM application, a visualization tool called HERMES was developed to allow near-realtime monitoring of GCM progress during a run. The data generated by applications such as GCM is very large; for example, the LANL POP program generated nearly 50 gigabytes of data for each simulated year. Prior to HERMES this data was typically not able to be meaningfully examined until a run was completed, which was very costly in situations where errors in initial conditions or instabilities invalidated the results. HERMES allowed scientists to monitor progress during the run while introducing an overhead cost of only about 15% to the run's wall-clock time for the additional I/O processing required to send data to the visualization workstation.
Chemical Process Optimization
Researchers at CMU in the Nectar testbed investigated the distribution of a chemical process optimization problem using heterogeneous metacomputing. The goal of this application is to improve the economic performance of chemical processing plants through optimal assignment of resources to processing units, and is representative of a large class of stochastic optimization problems in other fields. Real problems of interest have a combinatorially large solution space, and serial algorithm solutions have been limited by their computation time to relatively small problems.
The availability of a SIMD CM-2, a MIMD iWarp array, and a vector-based C90 in the Nectar testbed allowed CMU to implement new parallel algorithm solutions for the major parts of the problem, while executing vectorized tasks where appropriate on the C90. The set of algorithms used were not previously implemented in a form which allowed execution on a single machine, precluding a direct speedup comparison for this work.
The problem size for this application is determined by parameters representing raw materials, processing units, costs, and the number of samples and grid points used in the computations. For this investigation the number of samples and grid points were fixed and a single variable, n, used to represent problem size.
The solution has two phases: a data generation and analysis phase, followed by a Linear Assignment Problem (LAP) solution phase. The data generation reflects the real world modeling of the problem, and was done on the 64-node iWarp array located at CMU. As this computation proceeded, output data was sent to the C90 at the Pittsburgh Supercomputer Center (PSC), where a single CPU was used to analyze the data and compute cost matrix elements. This data was then sent to a 32K-node CM2 at PSC.
Phase two, LAP solution, began once all data from the first phase was received by the CM2. This phase consisted of three discrete steps: first the CM2 computed a reduced cost matrix used for LAP solver initialization and sent the results to the C90, which performed the next LAP computational step; these results were then sent back to the CM2 for the final stage of LAP solution processing (Figure 4-20).
Figure 4-20. Chemical Process Optimization
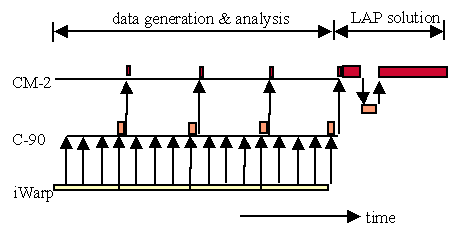
Parallel computation was possible in the first phase, which due to its one-way data flows allowed the iWarp to compute continuously and a simple pipeline to be formed. Because the cumulative execution times for both the C90 and CM2 were only a few percent of the execution time required by the iWarp in this phase, total time was relatively insensitive to the computational granularity used by the iWarp for passing data to the C90. For example, for a problem size of n=4000, the iWarp required 13 minutes for its total computation; when divided into 8 intervals, 500 MBytes was generated for transmission to the C90 in each interval. Since transmission of the data could be spread out over the iWarp computation interval, in this case a data rate of only 50 Mbps allowed communication to the C90 to keep up with computation (with smaller rates required for C90 to CM2 transfers).
In the LAP solution phase, a single two-way exchange was required between the CM2 and C90, with computation and communication occurring sequentially, precluding the use of pipelining. For the n=4000 problem size, total CM2 execution time was 3.2 minutes, C90 time was approximately 50 seconds, and for a data rate of 100 Mbps or higher the sequential data transfers did not significantly add to total LAP solution phase time.
To determine how solution times and data rate requirements scaled with more powerful machines, CMU researchers developed a set of analytical models based on trace data obtained from the experimental runs. The results showed that, as the number of iWarp nodes is increased, it ceases to be the bottleneck and total solution time becomes quite sensitive to network bandwidth. For a 1000-node iWarp machine (estimated to be roughly equivalent to a medium-sized Intel Paragon), a data rate of at least 800 Mbps is required to prevent its data transfers to the C90 from becoming a bottleneck.
Two issues of note in the experimental work concerned format conversions and machine availability. Floating point format conversions on the C90 for data received from the iWarp made up about 35% of total C90 execution time for first-phase processing. Although masked by total iWarp processing for the n=4000 case, the impact of this processing becomes significant as iWarp execution time is reduced.
Machine availability here refers to whether the machine was dedicated or shared during the run. For these experiments, the CM2 and iWarp processor arrays were dedicated while the C90 was shared with other jobs. Since C90 execution time was a small percentage of total time in both phases, its variability did not significantly impact the results: it was masked by the continuous iWarp processing in the first phase, and its impact on total time was less than 1.5% in the sequentially-executed second phase. While the C90 variability would have a greater impact as CM2 processing power is scaled up, this result demonstrates that tight coordination of all metacomputer machine resources is not required for some problems.
General Branch and Bound Problems
A Nectar testbed effort involving Purdue University researchers investigated a class of large combinatorial problems using the well-established branch and bound solution framework. Unlike the other distributed computation efforts discussed above, their work was based on homogeneous metacomputing using a network of workstations. Another difference was their focus on a general problem-solving solution rather than using a specific problem as the basis for their investigation.
Building on earlier distributed application work for particular branch and bound problems, they developed a software system for rapidly prototyping custom solutions for a large class of problems. Called DCABB (Distributed Control Architecture for Branch and Bound Computations), the software provides algorithm parallelization and distribution while also allowing the user to tailor the parallelization details to his or her specific problem. DCABB handles the details of assigning computation to individual nodes and the communications among them using a message-passing paradigm, and deals with problems such as node or network failures.
A special high level language called CLABB, Control LAnguage for Branch and Bound, was also developed to allow users to specify their particular algorithms. The CLABB specification is then parsed into a programming language such as C++, providing portability across a wide variety of platforms. The DCABB execution environment includes tools for monitoring and visualization of progress during a run, allowing the user to gain insights into changes needed for solution optimization.
The measure of problem size for this problem class is node size, the amount of information (in kilobytes) associated with each node of a problem's combinatorial tree. The node size reflects the number of elements and level of detail describing the problem, and is directly related to the amount of processing which must be performed for each node of the tree.
The time required to compute an individual tree node result defines the computational granularity of the distribution. DCABB distributes queues of tree nodes among the processors comprising the metacomputer, with data exchanged when a tree node computation is completed. The notion of pipelining is thus quite different for this case than the previously discussed applications -- work proceeds in parallel but asynchronously among the set of processors, with highly bursty data transfers taking place as processors become idle and tasks are redistributed. The associated data/control exchange topology is in general n-connected, as shown in Figure 4-21.
Figure 4-21. DCABB Data Exchange
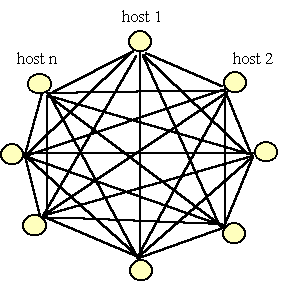
To explore the resulting system performance, a generic branch and bound search process was developed which generated combinatorial trees similar to those for many real problems. By manipulating a number of control parameters, this approach allowed more general results to be obtained than if tests had been carried out for a few specific problems. Data was obtained for a range of key parameters using a network of eight DEC Alpha 3000/500 workstations and two network configurations, the first consisting of a shared 10 Mbps ethernet and the second consisting of switched 100 Mbps links. By comparing results for the different bandwidths, the impact of communications on total problem solution time could be characterized.
Experiments were run for problem sizes of 10, 100, and 1000 KBytes and computational granularities (node execution times) of 20-40, 200-400, and 800-1000 milliseconds, where a smaller granularity represents a processing speedup due to a faster algorithm or more powerful processor. The results showed that, for a given network bandwidth and sufficiently large problem size, there is a point beyond which decreasing the granularity results in an increase in total solution time due to increased communication requirements.
For the 1000 KByte problem size, solution time in the ethernet case monotonically increased as granularity was decreased from 800-1000 to 20-40, implying that the problem was constrained by the network bandwidth for all granularities used. When this problem size was repeated using 100 Mbps links, total solution time was reduced by a factor of two for the 20-40 granularity relative to the ethernet case. The solution time was smallest for the 200-400 granularity value, rising again as the granularity was increased to the 800-1000 value. This implies that a still higher network bandwidth was required for this problem size to realize the speedup afforded by the 20-40 granularity.
The 100 KByte problem size showed a slight reduction in solution time with the higher bandwidth at the 20-40 granularity, indicating its bandwidth requirements were just beginning to exceed that provided by the ethernet at that point. For the 10 KByte problem size, the smallest solution time was obtained at the 20-40 point and increasing the bandwidth did not reduce this time further.
Overall, while DCABB's bursty communication requirements are difficult to characterize in detail, the experimental results demonstrated that bandwidths greater than 100 Mbps are needed for problem sizes on the order of 1000 KBytes or higher. Because of the non-overlapped n-way communication exchanges required, however, propagation latencies may impose limits on solution time reductions as bandwidths are increased beyond a certain point, particularly when wide area networks are used.
In addition to advancing our understanding of distributed computation using high speed networks, the DCABB work has produced an important methodology for solving large combinatorial problems. As a result of strong interest by industry, a company has been formed to develop and market a commercial version of DCABB directed at the solution of Mixed Integer Linear Programs, a technology widely used by manufacturing, retail distribution, and other industries.